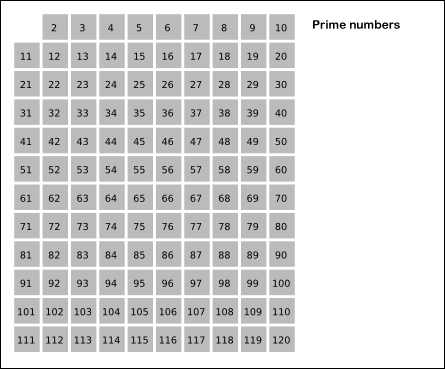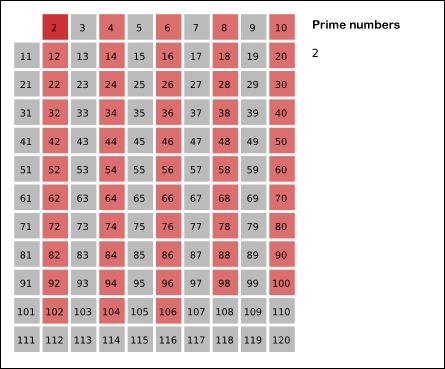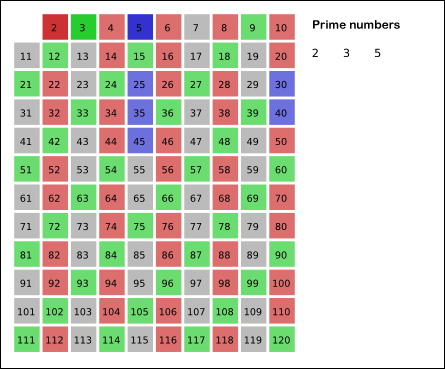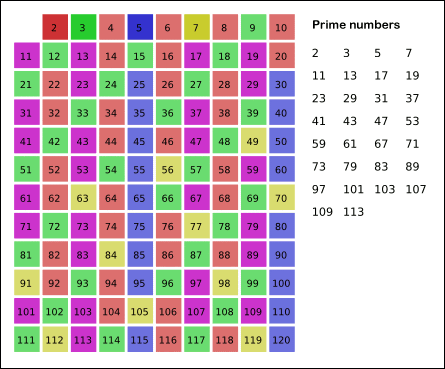
毕达哥拉斯质bai数是指可以表示为 4n + 1 形式的质数,若直角三角形的三边均为整数,斜边为质数,其斜边的边长即为毕达哥拉斯质数.
前几个毕达哥拉斯质数为
5,13,17,29,37,41,53,61,73,89,97,101,109,113,… (OEIS中的数列A002144).
费马平方和定理陈述,毕达哥拉斯质数可以表示为二个平方数的和,其他质数除了2以外(2=1^2+1^2)都不能表示为二个平方数的和.毕达哥拉斯质数及2会在高斯整数的范数中出现,其他的质数不会是高斯整数的范数.
毕达哥拉斯质数可以表示为一个奇数的平方数与一个偶数的平方数的和:
毕达哥拉斯质数是可以表示为a^2+4b^2形式的质数.
依照二次互反律陈述,若p及q为奇质数,其中至少有一个为毕达哥拉斯质数,则 p是模q的二次剩余的充份必要条件是q是模p的二次剩余 .相反的,若p及q都不是毕达哥拉斯质数,则p是模q的二次剩余的充份必要条件是q不是模p的二次剩余.−1是是模p的二次剩余的充份必要条件是p是毕达哥拉斯质数(或2).
在p为毕达哥拉斯质数的域Z/p中,多项式x^2 = -1有二个解.
标签: 素数
大素数密码
| 1 | 2 | |
| 2 | 7 | |
| 3 | 227 | |
| 4 | 632483 | 可以用快速筛法 |
| 5 | 11619640863583 | 使用欧拉函数,确定大概范围 二分法查找指定范围内的个数 当范围内个数只有一个时,这个就是目标素数 |
素数部分定理
1.素数本身只能被自身整除。也就是质数的约数只有两个,即1和本身。
2.所有大于3的素数,都可以用6n-5 和6n-1表达,或6n+1和6n+5来表示。
3.若”k”不是”6xy+x-y”的方程解,也就是”k≠6xy+x-y”,那么”6k-1″一定是个素数。 4.若”k”不是”6xy+-(x+y)”的方程解,也就是”k≠6xy+-(x+y)”,那么”6k+1″一定是个素数。
5.由3.和4.假设,素数集合是由两条元素不重复的独立集合。
6.质数的个数公式π(n)是不减函数。且素数的分布个数接近于x/ln (x),这是素数定理。
7.素数本身是不可能有传统意义上的通项公式。
8.任一大于1的自然数,要么本身是质数,要么可以分解为几个质数之积,当代入1时候这种分解是无限的,去掉1时分解则是唯一的。
9.质数的个数是无限的。
10.所有大于10的质数中,个位数只有1,3,7,9。
11.若n为正整数,在n^2到(n+1)^2之间至少有一个质数。
12.若n为大于或等于2的正整数,在n到n!之间至少有一个质数
13.若质数p为不超过n(n≥4)的最大质数,则p>n/2。
14.两个连续素数最大间隔可以任意大。
15.任意大于5的奇数都可以表示为三个素数之和。