正整数倒数的前n项和形式是这样的.
数学家和广大的数学爱好者凭着过往积累的自信,认为应该也能推导出一个公式来计算上式,这个自信来自于下面的事实.
我们能求正整数的前n项和.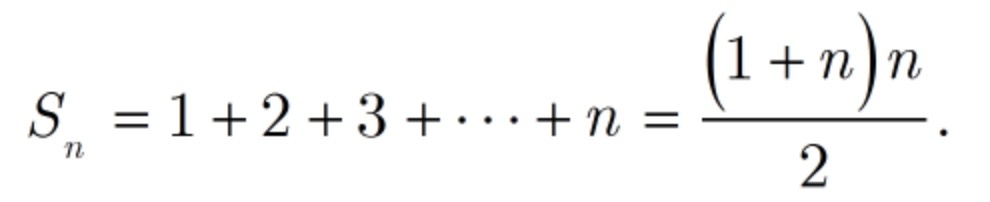
我们能求正整数平方的前n项和.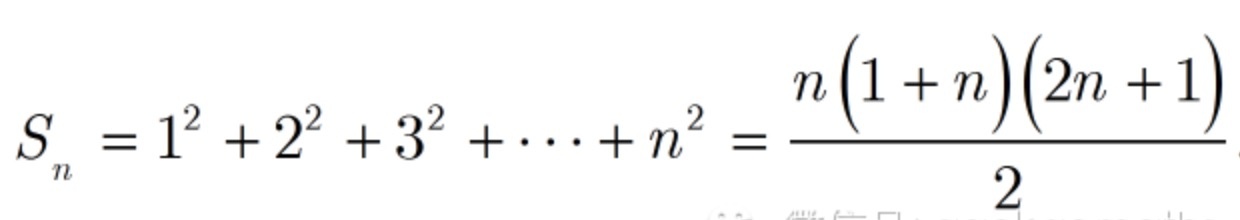
我们能求正整数立方的前n项和.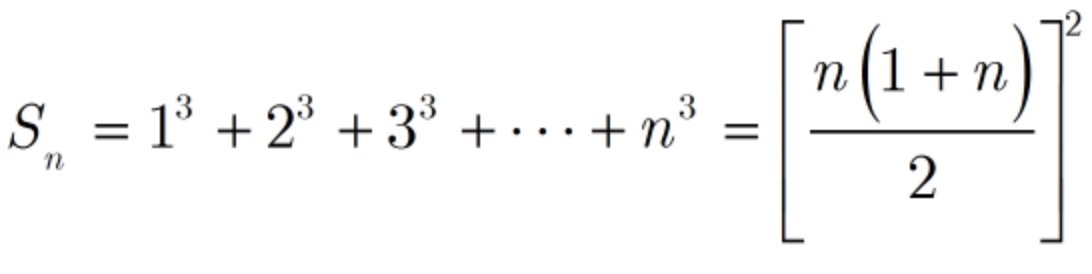
可是,几百年的实践至今,我们依然找不到合适的公式去计算从1开始的连续的正整数的倒数和.
近似估计
正整数的倒数数列也称为调和数列.这个无穷数列的和是发散的.
但并不说,数列发散就没有求和公式.比如,正整数数列也是发散的,但显然有求和公式;首项大于0、公比大于1的等比数列也是发散的,但也有求和公式.
不管怎样,这个调和数列目前就是没有找到合适的求和公式.我们只能尝试去估计它的范围.
当n很大的时候,我们能够用下面的公式去估计它.
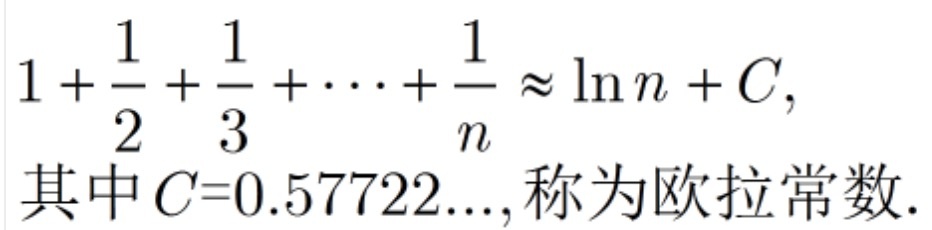
但是,在我们目前学到的初等数学中,如何处理这类求和问题呢?
基本的思想就是,通过适当地放缩,放缩为能够求和的形式,最后研究这个和式的范围.
用函数不等式实现放缩
能够用于放缩的不等式有: lnx<=x-1 (当且仅当 x=1时取等号)
然后采用赋值的方法朝正整数的倒数和靠近.

以上是朝小的方法去放缩,如果我们希望朝大的方向去放缩呢?

总结,用放缩法得出正整数前n项倒数和的范围是
