作者： liyunde

什么是江湖飘门律？说起来很复杂，不是三言两语能讲清楚的。是旧时代走江湖的飘门卖艺人所遵循的一条行为准则，它与官方法律不一样，事实上是超出正常法度之外的一条容忍底线。
俗话说强龙不压地头蛇，走江湖的卖艺人就算有一身功夫，也不会轻易去惹麻烦。走江湖流浪各地。对地方上的各种帮会势力，遇上了通常都要拜码头，否则在人家的地盘上不好做生意。如果受了什么欺压。一般都会选择回避或忍让，尽量不起冲突。
就算有一身好功夫，假如真起了正面冲突，生意做不成不说，在不明底细的地方对付不明底细的势力，说不定会有无穷无尽的后患。但这种回避与忍让并不是没有底线的。在什么情况下江湖飘门中人一定会动手呢？
面对欺压做出退让的选择无非是两种情况，一是你低头对方也知道收手，二是即使你低头对方也不会手软。在第二种情况下不论你怎么回避，对方都不会放过你，如果不是对手的话，那就赶紧逃走吧。如果有那个能耐，或者就算不是对手也实在躲不掉，那就出手！
这就是江湖飘门律。
至于出手的后果如何，已经没法过多的考虑了，毕竟刀已经架在眼前。而六扇门的人还没有追到身边。

物理定义：熵增过程是一个自发的由有序向无序发展的过程(Bortz, 1986; Roth, 1993)。 热力学定义：熵增加，系统的总能量不变，但其中可用部分减少。

统计学定义：熵衡量系统的无序性。熵越高的系统就越难精确描述其微观状态。

早在1943年，在爱尔兰都柏林三一学院的多次演讲中，薛定谔就指出了熵增过程也必然体现在生命体系之中，其于1944年出版的著作《生命是什么》 中更是将其列为其基本观点，即“生命是非平衡系统并以负熵为生。”

人体是一个巨大的化学反应库，生命的代谢过程建立在生物化学反应的基础上。从某种角度来讲，生命的意义就在于具有抵抗自身熵增的能力，即具有熵减的能力。在人体的生命化学活动中，自发和非自发过程同时存在，相互依存，因为熵增的必然性，生命体不断地由有序走回无序，最终不可逆地走向老化死亡。

熵的定义

熵，热力学中表征物质状态的参量之一，用符号S表示，其物理意义是体系混乱程度的度量。

（1）经典热力学
1865年，克劳休斯将发现的新的状态函数命名为熵，用增量定义为 ，式中T为物质的热力学温度；dQ为熵增过程中加入物质的热量。若过程是不可逆的，则 ，下标“ir”是英文单词“irreversible‘’的缩写，表示加热过程所引起的变化过程是不可逆的。

合并以上两式可得 ，此式叫做克劳休斯不等式，是热力学中第二定律最普遍的表达式。

（2）统计热力学
熵的大小与体系的微观状态Ω有关，即S=klnΩ，其中k为玻尔兹曼常量，k=1.3807×10-23J·K-1。体系微观状态Ω是大量质点的体系经统计规律而得到的热力学概率，因此熵有统计意义，对只有几个、几十或几百分子的体系就无所谓熵。

熵的性质

（1）状态函数熵S是状态函数，具有加和（容量）性质（即对于系统M可分为M1与M2，则有SM=SM1+SM2），是广度量非守恒量，因为其定义式中的热量与物质的量成正比，但确定的状态有确定量。其变化量ΔS只决定于体系的始终态而与过程可逆与否无关。由于体系熵的变化值等于可逆过程热温商δQ/T之和，所以只能通过可逆过程求的体系的熵变。孤立体系的可逆变化或绝热可逆变化过程ΔS=0。

（2）宏观量熵是宏观量，是构成体系的大量微观离子集体表现出来的性质。它包括分子的平动、振动、转动、电子运动及核自旋运动所贡献的熵，谈论个别微观粒子的熵无意义。

（3）绝对值熵的绝对值不能由热力学第二定律确定。可根据量热数据由第三定律确定熵的绝对值，叫规定熵或量热法。还可由分子的微观结构数据用统计热力学的方法计算出熵的绝对值，叫统计熵或光谱熵。

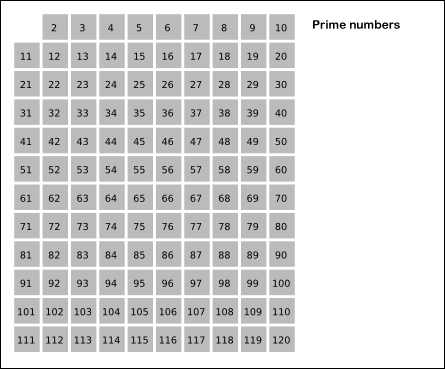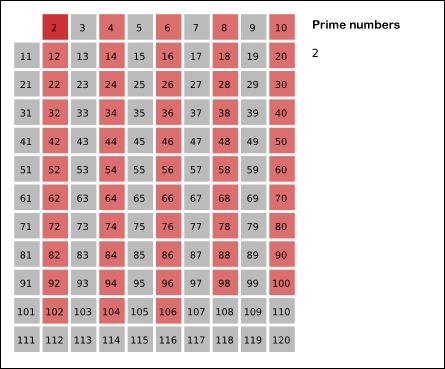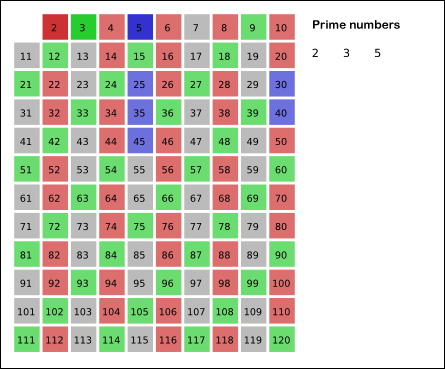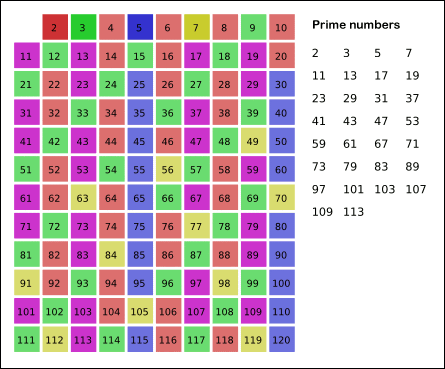
原文:https://bbs.pinggu.org/thread-7046070-1-1.html

在1998年亚马逊致股东信里，贝佐斯说：“我们要反抗熵（We want to fight entropy）。”

管理学大师彼得·德鲁克说：“管理要做的只有一件事情，就是如何对抗熵增。在这个过程中，企业的生命力才会增加，而不是默默走向死亡。”

物理学家薛定谔说：“自然万物都趋向从有序到无序，即熵值增加。而生命需要通过不断抵消其生活中产生的正熵，使自己维持在一个稳定而低的熵水平上。生命以负熵为生。”

这么多人都在谈论熵，说要反抗熵，然而到底什么是熵？

什么是熵？

熵，是来自于物理学热力学第二定律的一个词。

当一个非活系统被独立出来，或是将它置于一个均匀环境里，所有运动就会由于周围各种摩擦力的作用很快停顿下来；电势或化学势的差别会逐渐消失；形成化合物倾向的物质也是如此；由于热传导的作用，温度也逐渐变得均匀。由此，整个系统最终慢慢退化成了毫无生气、死气沉沉的一团物质。

于是，就达到了被物理学家们成为的“最大熵”，这是一种持久不变的状态，在其中再也不会出现可以观察到的任何事件，它已经归于死寂。

熵代表了一个系统的混乱程度，或者说是无序程度 – 系统越无序，熵值就越大；系统越有序，熵值就越小。

所以，负熵代表着系统的活力，负熵越高就意味着系统越有序，这也是为什么薛定谔会说“生命以负熵为生”。

比如：在每周刚刚开始的时候，我们都会把房间收拾得窗明几净，可是一到周末，我们就会发现房间乱成一团。这个过程就是熵增的过程。

再比如：生命有机体在不断进行的吃、喝、呼吸以及（植物的）同化，也就是新陈代谢，正是一个对抗熵增的过程。

不要小看这个听起来非常朴素的熵定律，它在自然界中无处不在，是最基本也最重要的一个法则，化学家阿特金斯曾将它列为“推动宇宙的四大定律”之一。

它是物理学家心目中无比坚定的一个信仰，连引力公式都可以改写，但熵增定律却从未被违反。张首晟教授认为，人类的知识再往前推进，牛顿力学可能不对，量子力学可能不对，相对论可能也不对，但信息熵的公式却是永恒的。

如果将它推论至整个宇宙的发展中，我们就会发现：如果我们存在的这个宇宙之外什么都没有，也就是如果没人向这个宇宙输入能量的话，宇宙的最终结局就是走向彻底的无序，也就是死亡。

如果将它推论到企业管理中，我们就会发现：管理要做的只有一件事情，就是如何对抗熵增。如果没能有效对抗熵增，企业就会在默然中走向死亡。

如果将它推论到人生之中，我们就会发现：如果不去对抗熵增，我们的生命力就会在封闭系统内或平衡状态中逐渐变得毫无生气、死气沉沉。

那时，即使生命尚未终结，生命力也已戛然而止，也就印证了那句著名的话“很多人20岁时就已死去，到80岁才埋”。

然而，我们又该如何对抗熵增呢

  对抗熵增的 人生底层逻辑

想要对抗熵增，就要引入一个非常重要的理论- 耗散结构。

“耗散结构”是由一位名叫普利高津的科学家提出的，他也因为这个理论而获得了1977年的诺贝尔化学奖。

什么是“耗散结构”？

耗散结构是一个远离平衡态的非线性的开放系统（不管是物理的、化学的、生物的乃至社会的、经济的系统），通过不断地与外界交换物质和能量，在系统内部某个参量的变化达到一定的阈值时，通过涨落，系统可能发生突变即非平衡相变，由原来的混沌无序状态转变为一种在时间上、空间上或功能上的有序状态。

耗散结构有两个最为重要的特性，一是开放性；二是非平衡。当一个系统具备了“耗散结构”后，它就能够有效对抗熵增。

那么，我们该如何依据这样两个特点将自己打造成一个可以对抗熵增的“耗散结构”呢？1

开放性

一个孤立系统的熵一定会随时间增大，当熵达到极大值时，系统就会达到最无序的平衡态，所以孤立系统绝不会出现耗散结构。

因此，耗散结构一定产生于开放系统，它必须存在着由环境流向系统的负熵流，而且能够抵消系统自身的熵增，只有这样才能使系统的熵减小，有序度增加。

维基百科与网络版的大英百科全书，都很专业，而维基百科却不需要有一群专家进行搜集编撰，它是一个开放系统，每个人都能为它贡献内容。也正因为此，它甚至拥有比网络版大英百科全书更高的传播度。

那么，我们该如何让自己成为一个开放系统呢？

1）用“成长型思维”替代“固定型思维”

很多人一直保持着这样一种观念，即我们天生有一些特定的固定不变的能力与品质，就像“我不善于运动”、“我没有学数学的天分”等，因此无法改变。

但真是这样吗？

实际上，人的智力、创造力、运动才能与其他品质，都是可以锻造的，是可以通过时间和努力去改变的。

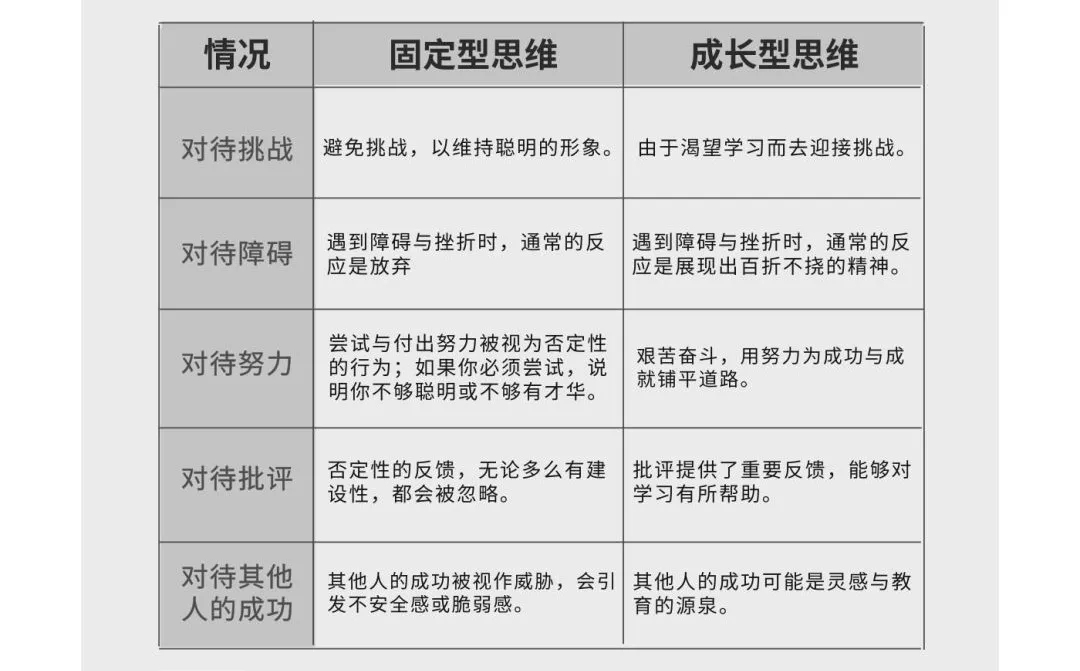
2006年，斯坦福大学的行为心理学教授卡罗尔·德韦克出版了一本名为《思维模式：新成功心理学》的书。在这本书中，德韦克总结了自己30多年的研究成果，提出了两种思维理论：固定型思维和成长型思维。

固定型思维说的是，相信我们出生时带有固定量的才智与能力。采取固定型思维的人倾向于回避调整与失败，从而剥夺了自己过上富于体验与学习的生活。

而成长型思维则是一种以智力可塑为核心信念的系统的思维模式。它相信通过练习、坚持和努力，人类具有学习与成长的无限潜力。

拥有成长型思维的人能够沉着应对挑战，他们不怕犯错或难堪，而是专注于成长的过程。他们对于失败不害怕，因为他们知道从失败和错误中学习，它们终将变为成功。

正如科研大数据所告诉我们的：如果一个孩子拥有成长型思维，这项优势就可能消除最富有家庭与最贫穷家庭间的差距，因为成长型思维的孩子会越来越优秀。

从这个图表中，我们还能看到一点，也许是我们平时常常忽略的，那就是二者在对待其他人的成功这点上还有不同：成长型思维的人会将别人的成功当做自己的灵感，而固定型思维的人则会将别人的成功当做是对于自己的威胁，于是就会引发巨大的不安全感以及脆弱感。而这样一种不安全感和脆弱感，常常会让他选择堵住耳朵，闭上眼睛，于是也就切断了自我成长的渠道与途径，让整个情况变得更糟。

2）用“流量思维”代替“存量思维”

躺在书桌上的一堆油画颜料，不会自动变成一幅美妙的油画。一定是因为有了某种外界能量交换，比如，你拿起了画笔，打开了颜料，开始画画，颜料才能变成油画。

这是什么意思？

意思是说，只有在与外界交换能量之后，一个人才有可能发生翻天覆地的变化。这样的人就是有着“流量”思维的人，相反则是“存量思维”。

什么是“存量”思维者的典型行为？

相比在学习上给自己做出投资，他更愿意把钱存起来，让它产生利息；相比换个更适合更有前途的岗位或行业，他更愿意继续做现在这个安稳舒适的工作；相比将自己看到的好文章、好书推荐出去，他更愿意悄悄的收藏起来；相比与那些优秀者深入交流，他更愿意不让别人知道自己的想法。

可惜，如此一来，熵增就会加剧，危机就会潜伏。按照“熵增定律”，熵是繁荣有序的反面。然而，从表面来看，繁荣有序却是熵的隐性状态。

因此，当我们看到繁荣有序的表象时，以为熵并不存在，但实际恰恰相反，熵正在暗中窥伺。它不是不存在了，它只是隐形了。

1975年，24岁年轻的柯达工程师史蒂夫·萨松发明了世界上第一台数码相机，当他把这项惊人的成果呈现给公司高层的时候，傲慢的管理层对这个只能拍100·100像素的奇怪机器嗤之以鼻—“没有人愿意在电视上看他们的照片”，彼时的柯达在胶片时代笑傲群雄。

30十多年后，当柯达在2012申请破产保护的时候，当年的决策者们不会想到，敲响他们丧钟的正是他们自己公司发明并雪藏起来的数码相机。

历史总是惊人的相似，同样的事情还发生在了摩托罗拉和诺基亚的身上。死守“存量”，蔑视“流量”，终会带来“当下很好、未来很糟“的必然结果，而这个结果往往不是一般人能够承受的，就像清政府当年的”闭关锁国“政策一样。

2012年的时候，任正非有个非常重要的讲话，叫做《华为的2012》。

听起来他好像是在唱衰华，其实不然，他只是比较清醒地意识到华为作为一个企业，和所有其他企业一样，始终有一个巨大的威胁存在着，它就是熵。所以，任正非认为只要华为存在一天，都必须得对抗熵增。

他对华为也是这样做的：在华为的研发上做出巨额投入，比如华为2017年在研发上的投入超过900亿元的情况，研发投入占收入的近16%，这个研发的投入强度，可能比阿里和腾讯的研发投入总和都要大，更是超过了苹果。过去10年累计投入研发2400亿人民币，华为也已连续多年都是全球专利申请第一名。

从1997年开始，华为就开始持续引进来自外部的管理经验，包括IBM、埃森哲、波士顿咨询等。他们陆续给华为提供了多方面的变革，使华为在管理创新、组织机构创新、流程变革方面不断进步，奠定了华为成为一家全球化公司的根基。

这些，都是在用“流量思维”代替“存量思维”，作为一家国内知名公司，即使不做巨额科研投资，也可以既有“存量”为荣；然而，华为却并不这么想，它看到的是“流量”，是开放系统所需要的能量交换。

3）用“终身学习”代替“临时学习“，用”终身探索“代替”不再探索“

有人，每天都在学习，不论是多还是少。有人，偶尔学习一次，看一本书要用七八个月。

前者，我称之为“终身学习者”，后者，我称之为“临时学习者”。学习对于前者如同呼吸一般，对于后者则如同救急的膏药，只在受到刺激或工作需要之时，才会想起。

对于“终身学习者”而言，他通过每天学习，将自己打造成了一个开放的系统，并且能够产生复利效应。

对于“临时学习者”而言，他是封闭的体系，无力对抗熵增，也无法产生复利效应。短期内自然看不出来，但是长期来看，二者却有天壤之别。

很多人，在成年之后就不再探索了，他们停止了对于这个世界，以及对于自我的探索，他们只想走在那条早已明确的路上，按部就班的生活。但却不知，根据熵增定律，熵的阴影早已紧随其中，“中年危机”的到来也不过只是时间问题。

而那些”终身探索者“呢？

他们则很不同，他们对于这个世界、对自我、对他人，都始终有着浓烈的好奇之心，他们想要探索那些不懂的东西，想要解开那些难解的奥秘；不论是从一场电影、一次旅行、一本杂志，还是一次对话，他们都能从中探索到新鲜的信息、知识或智慧。他们就像是一些敞着口的容器，在贪婪的吸取着来自于外部世界的一切。

所以，如果想将自己打造成“开放系统”，就需要做到至少三件事：

• 第一，用“成长型思维”代替“固定型思维”。
• 第二，用“流量思维”代替“存量思维”。
• 第三，用“终身学习”代替“临时学习”，用“终身探索”代替“不再探索”。

2

远离平衡态

远离平衡态是“耗散结构”的第二个特点。

平衡态是指在没有外界影响条件下，热力学系统的各部分宏观性质在长时间里不发生变化的状态。

“耗散结构”的提出者普利高津认为，非平衡是有序之源。

那我们该怎样才能远离平衡态呢？

1）从“舒适区”走进“学习区”，甚至“恐慌区”

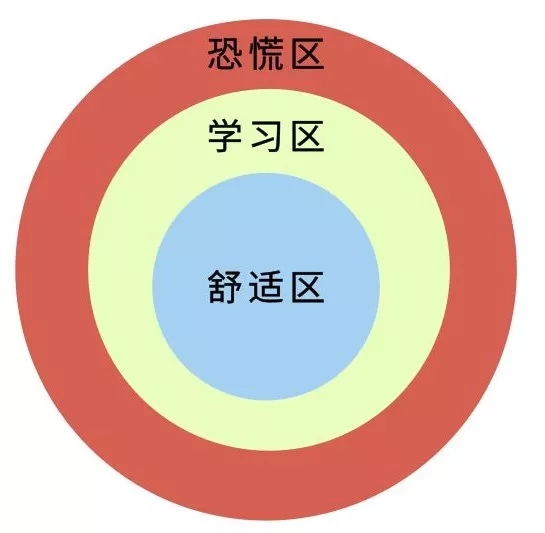
“舒适区”是美国人NoelTichy提出的理论，图里的3个区可以表示为你想学习事物的等级：

最里面一圈是“舒适区”，它代表的是对你来说没有学习难度的知识或者习以为常的事务，自己可以处于非常舒适的心理状态。

中间一圈是“学习区”，它代表的是那些对你来说有一定挑战，因而感到不适，但是不至于太难受的工作、学习、思考。

而最外一圈则是“恐慌区”，它代表的是超出你能力范围太多的事务或知识，心理感觉会严重不适，可能导致崩溃以致放弃学习。

在舒适区里，你能得心应手，因为每天都是处在熟悉的环境之中，做着自己在行的的事，和熟悉的人交际，甚至你就是这个领域的专家，对这个区域中的人和事感到非常舒适。

这就是暂时的“平衡态”，因为你无需过多努力就能使所有事物都达到一个相对平衡、比较舒适的状态。

然而，不要忘了，平衡态正是熵最大的时候。

这时，你学到的东西很少，进步缓慢，缺乏挑战和流动。这是一个看似平稳安逸，但却危机重重的状态，也就是“假性繁华”。

如果想要对抗人生熵增，按照耗散结构，你就须得远离平衡态，也就是离开那个让你感到非常舒适的区域，主动走向“学习区”，甚至是“恐慌区”。

亚马逊CEO贝佐斯就是这样做的，他将亚马逊的自营电商业务扩展到AWS云服务、FBA物流体系。而且，亚马逊在做自营电商的时候，还大胆引入了第三方卖家，让他们都在亚马逊上开店，跟自己的自营店竞争。亚马逊以网上卖书起家，但贝佐斯依然不甘心，开发出kindle阅读器用电子书打败自己的纸质书。

如果亚马逊只是停留在自己看似非常强大的自营电商业务里，在一段时间内，它当然能够获得不错的利润，达到一种稳固的平衡态。

但是，随着时间的推进，企业一定会越来越缺乏活力，缺乏创新，最终走向死亡。

正是因为贝佐斯非常清楚“熵”对于一个企业的严重危害，所以他在努力将亚马逊每一次好不容易建立好的平衡感推倒，不断把钱、把资源投入到新的领域；在企业内部创造各种形式的竞争。

也正因为此，亚马逊创造了重量级的明星业务，贝佐斯也成为了全球首富，这就是远离平衡态的巨大力量。

2）颠覆式成长

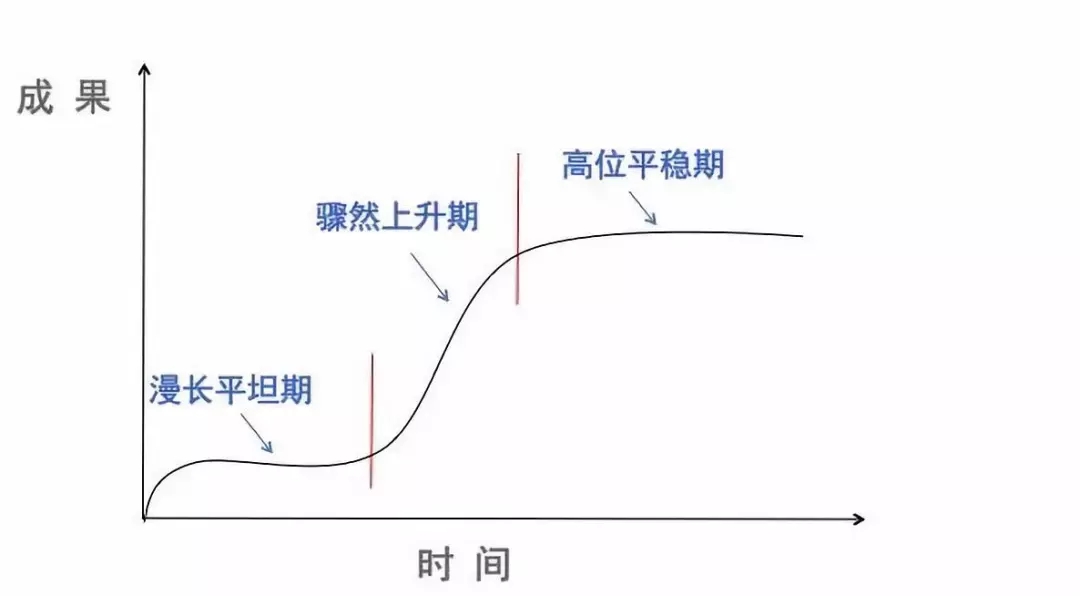
个人成长遵循的是S型曲线，在刚开始的时候，会有非常漫长的平坦状态，而后则会如火箭般骤然升空，并最终在高位保持平稳。

但这还不是颠覆式成长。

颠覆式成长不仅是一次S型曲线的飞越，它是很多次的飞越，它要求我们在完成一次S型曲线的增长后，再进入到第二条S型曲线，重新来过，不断颠覆自我。

2007年，IPOD占苹果公司收入的50%以上，iTune占74%的市场份额。按理说这正是一个产品如日中天之时，正常人的思路肯定是要继续做这个产品，用它好好赚钱。可乔布斯倒好，他要亲手颠覆掉这个已经大获成功的产品。

于是，他又做了iPhone，到2012年的时候，iPhone已经占到了苹果收入的58%，利润占到了70%。这就是乔布斯的“颠覆式成长”，他用自己做的iPhone颠覆掉了自己做的IPOD。他用一条新的S型曲线，颠覆掉了好不容易攀爬上去的S型曲线。

想要远离平衡态也是如此，需要一次又一次的走在漫长的平路上，然后跃上巅峰，在好不容易跃上巅峰之后，又要开始第二条S型曲线，就这样，不断进行自我颠覆。

而这种自我颠覆之所以很难，是因为当我们一旦到达S型曲线的上方平台，惰性就会产生。这时，是某阶段职业生涯的巅峰期，是某阶段自我发展的巅峰期，是一个看起来非常不错的状态。然而，如果一旦在这个平衡态停滞，你便不再获得成长与进步，最终的结局就是熵增加剧。

于我而言，在工作后至少做过几次非常大的颠覆式成长。

从销售部到市场部，后又从市场部到销售部；从以前在职场工作，到现在的自主工作，每一次都是颠覆式的成长。

在每一次颠覆式成长的过程中，从来都不是一帆风顺的，每次都会遇到很多的困难和阻碍，以及随之而来的孤独感与恐惧感，但得到的收获却是非常巨大的，我的人生也随之得到了极大的拓展。

那么，现在就来总结一下，两个远离平衡态的方法：

• 第一，离开舒适区，走进学习区，甚至是恐慌区。
• 第二，颠覆式成长。

这就是物理学中的熵增定律带给我们的人生底层逻辑 – 终其一生，我们都要对抗熵增，不然我们的生命力就会在默然中走向消亡。

而对抗熵增的方法就是：将自己打造成一个兼具“成长型思维”、“流量思维”、“终身学习、终身探索”、远离舒适区、能够持续颠覆式成长的耗散结构。