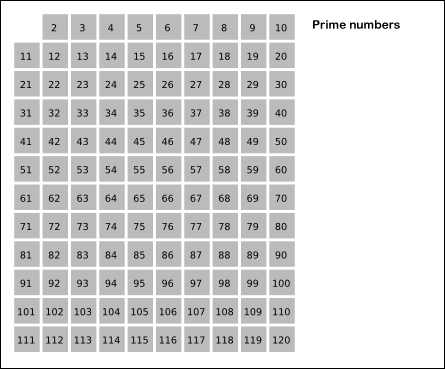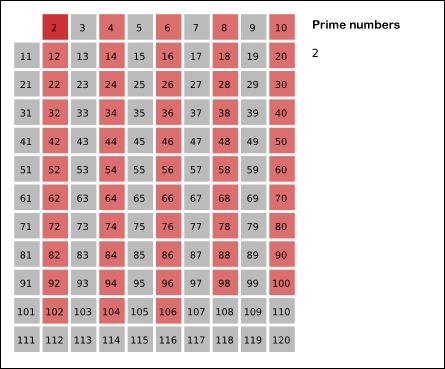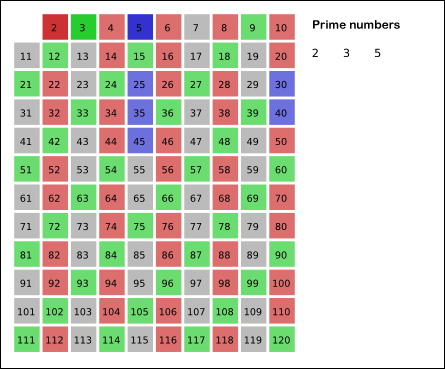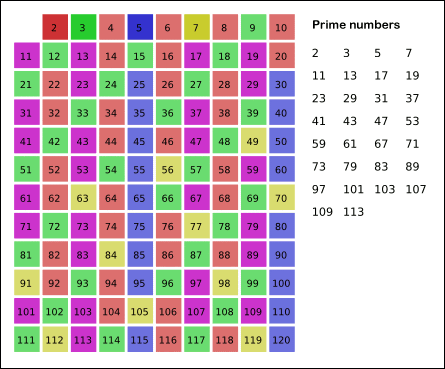
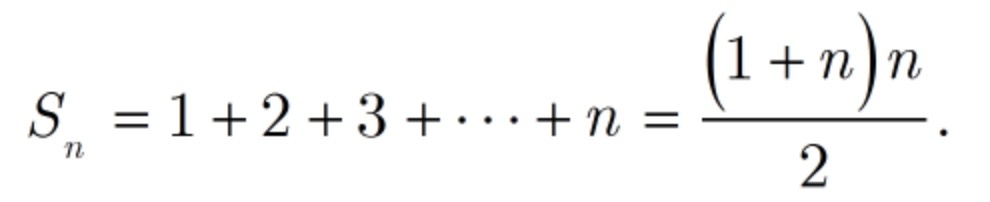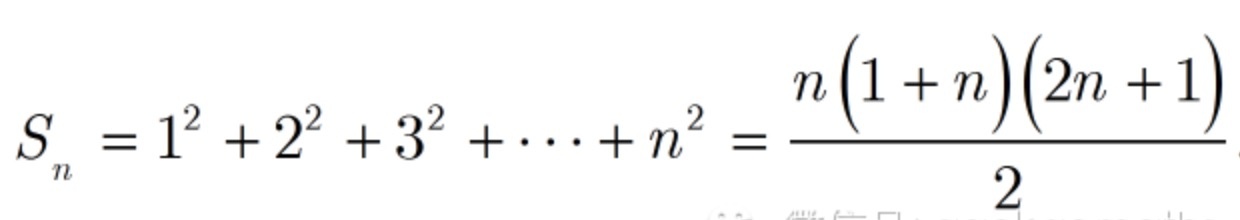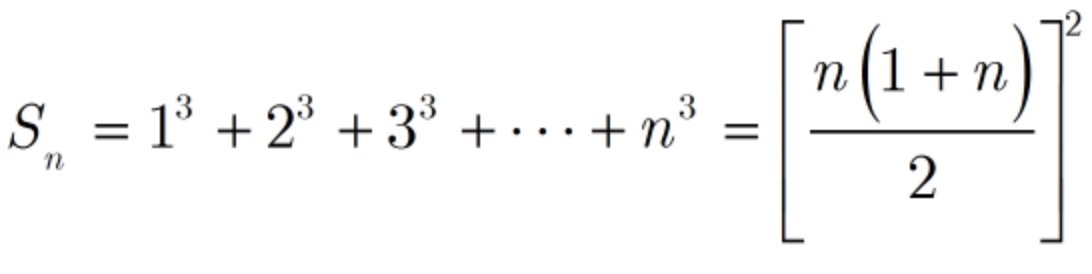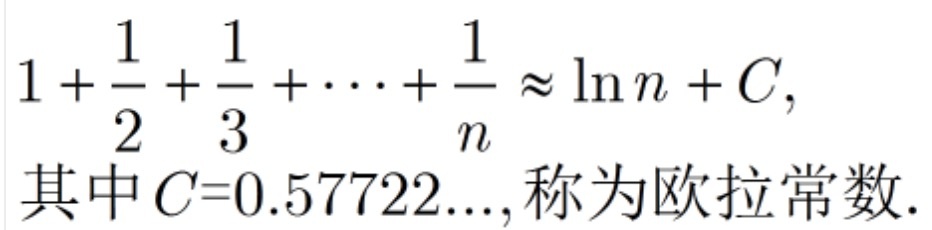记法
设n为正整数,a和b为整数,若a和b被n除后所得余数相同,
称a和b模n同余,记为a≡b(mod n);或 a≡b(% n)
此式被称为同余式。
或表达为:a % n =b % n 或 a mod n =b mod n;
若n能整除a则同余式表示为a ≡ 0(mod n)。
欧拉函数
对于正整数N,少于或等于N ([1,N]),且与N互质的正整数(包括1)的个数,记作φ(N)。即欧拉函数。
欧拉定理:
若N>2; a与N互质,则a^(φ(N)) ≡ 1 (mod N )
欧拉函数的性质:
(1) p^k型欧拉函数:
若N是质数p(即N=p), φ(N)= φ(p)=p-p^(k-1)=p-1。
若N是质数p的k次幂(即N=p^k),φ(N)=p^k-p^(k-1)=(p-1)p^(k-1)。
(2) mn型欧拉函数
若m,n互质,φ(mn)=(m-1)(n-1)=φ(m)φ(n)。
(3) 特殊性质:
若n为奇数时,φ(2n)=φ(n)。
费马小定理:
设任意整数a和素数p互素 ,则 a^p-1 ≡ 1(mod p)
运算规则
模运算与基本四则运算有些相似,但是除法例外。其规则如下:
(a + b) % p = (a % p + b % p) % p (1)
(a - b) % p = (a % p - b % p) % p (2)
(a * b) % p = (a % p * b % p) % p (3)
(a^b) % p = ( (a % p)^b ) % p (4)
结合率:
((a+b) % p + c) % p = (a + (b+c) % p) % p (5)
((a*b) % p * c)% p = (a * (b*c) % p) % p (6)
交换率:
(a + b) % p = (b+a) % p (7)
(a * b) % p = (b * a) % p (8)
分配率:
((a +b)% p * c) % p = ((a * c) % p + (b * c) % p) % p (9)
重要定理
若a≡b (% p),则对于任意的c,都有(a + c) ≡ (b + c) (%p);(10)
若a≡b (% p),则对于任意的c,都有(a * c) ≡ (b * c) (%p);(11)
若a≡b (% p),c≡d (% p),则 (a + c) ≡ (b + d) (%p),(a - c) ≡ (b - d) (%p),
(a * c) ≡ (b * d) (%p),(a / c) ≡ (b / d) (%p); (12)
若a≡b (% p),则对于任意的c,都有ac≡ bc (%p); (13)
RSA中重要的推论
m 和 n 是互质的正整数,则:
(a^m) %n = ((a%n)^m) %n
推论证明
a^m % n
=a*a ^(m-1) %n
=(a%n) *(a ^(m-1) %n ) % n //后续不断展开,一直至a ^0,即共有m项
=((a%n)^m) %n
推论中举例:
比如:2^3 mod 5
= (2 mod 5)^ 3 mod5
= 8 mod5
= 3
还有:3^3 mod 2
= (3 mod 2) ^3 mod 2
=1^3 mod 2
=1
加密思路:加密本质上是对加密内容的字节数组进行加密。不是对字符的本身进行加密。这样,整数对整数就可以进行相关的变换,即加密了。
比如:"I love Rust,Julia & Python, they are so cool! "的字节数组为:
[73, 32, 108, 111, 118, 101, 32, 82, 117, 115, 116,
44, 74, 117, 108, 105, 97, 32, 38, 32, 80, 121, 116,
104, 111, 110, 44, 32, 116, 104, 101, 121, 32,
97, 114, 101, 32, 115, 111, 32, 99, 111, 111, 108, 33, 32]
RSA加密算法为:
(1) 取两个大素数p,q (保密);
(2) 计算 n=p*q (公开), φ(n)=(p-1)*(q-1) (保密);
(3) 随机选取整数e,满足 gcd(e, φ(n))=1 (e与φ(n)互素)(公开);
(4) 计算 d 满足 d*e≡1 (mod φ(n)) (保密); (d为e的逆元,可通过扩展的欧几里得算法进行求解)
(5) {e,n}为公钥,{d,n}为私钥,也可以用{e,d}表示密钥对
(6) m为加密内容(如73),此时c为加密后的密文;
加密时 c = m^e mod n
解密时 m = c^d mod n
(7) m为签名内容,
签名时c = m^d mod n ;
解密时 m = m^e mod n
为什么RSA算法能保证其安全性?
要破解m =>
必须知道 d或e =>
必须知道 φ(n) =>
必须知道 p及q; =>
必须能破解 n=p*q =>
大质数因式分解的难度 => 公认
RSA证明
主要要证明m是否c^d mod n。由c = m^e mod n 。设M =m^e
证式
= c^d mod n
= (m^e mod n )^d mod n
= (M mod n) ^d mod n
= M^d mod n //见上面的推论
= m^(d*e )mod n ;
因为 d*e≡1 (mod φ(n))
得到:d*e =k *φ(n) +1 ; k是正整数。
上面证式还有,
= m^(k *φ(n) +1 ) mod n
= m^(k *φ(n))*m mod n //
= (m^(k *φ(n))mod n ) *(m mod n) mod n // 乘法
= 1 * m mod n // 由欧拉定理
= m
证毕。
所以解密的公式是对的。